Simulation of the Epidemiological Map of Covid-19 based on Ising Model by using Statistical Physics
Author
Abstract
Many types of research on Covid-19 have been recently carried out to investigate its spread and the ways
of its prevention. COVID-19 spreads from one to one during little droplets that a one with Covid-19
secretes from his snout or his maw when he sneezes, speaks, or coughs.
For containment of the disease spread, the model in statistical physics, Ising model on (100 x100) square
lattices, with the external magnetic field at temperatures very low and temperature very high (kBT=J =
2.0,99.0) infinite times equal to (1-hour, 12 hour, 24hour, and one week). Random-field Ising magnet was
used, every node of the square lattice carries a random-field Ising magnetic field ±h which is randomly up.
Our Simulation in this work is based on the normal Ising model, where, the external magnetic field in the
Ising model is presented by the carrier medium, the temperature is represented by the room temperature,
the number of nodes in the lattice size is presented by the persons (infected and noninfected) and the spinup represented to non-infected person who COVID-19 free or spin-down presented to an infected person
who has covid-19.
The extension conclusion for energy goes to up nodes as covid-19 free and down-spins had COVID-19
At lower temperature (2.0K) with a lower external magnetic field (0.10), there are many pictures,
distinguish between developing and non-developing areas, but for a lower temperature (2.0K) with a
higher external magnetic field (0.90), more pictures, distinguish between developing and developing areas.
With higher temperature (99.0K) and higher external magnetic field, we can't notice growing domains,
which tells us if the population, with COVID-19 or not, Implementation of preventive measures (wearing a
mask, maintaining safe distances between people), the spread of the disease is controlled.
Keywords
Epidemiological Map, Ising Model, Covid-19, Carrier medium.
1. Introduction
Coronavirus disease (COVID-19) is rapidly spreading which an infectious disease caused by a newly discovered coronavirus. The disease-spreading predictions open the research door for scientists, politicians, and industy.
We believe our paper is considered to be a basis to find out the disease spreading rate.
Now we know that SARS-CoV-2 is a new race that was unknown before, and the first person had infected with COVID-19 in Wuhan, China, in December 2019 [1,2,3]. After this knowledge, The World Health Organization (WHO) announced a pandemic of COVID-19. Currently, more than 179.075.604 cases and more than 3. 876. 675 deaths have been recorded worldwide [4].
In the field of epidemics, every hour counts, and there is a strong need to foresee the disease's temporal evolution to choose the best course of action and maintain proper control over its spread.
It was found that most mathematical modeling done were based on the Susceptible-Exposed-Infected-Removed (SEIR) and Susceptible-infected-recovered (SIR) models.
Statistical simulation and many modelling are central to infectious disease epidemiology.
Computer simulation of statistical models is one of the most important methods for analysing epidemiological maps of infectious diseases, which enables us to analyse disease dynamics and methods of spread, and accordingly, the Ising model was used to describe some aspects of transmission of a new disease. [5,6,7].
We are working in many researches in sociophysics [8-14].
All models of statistical physics are not used to explain how the COVID-19 is spreading, thus in our study, the modification of the Ising model has been used to describe the Covid-19 spread.
2. Materials and Methods
2.1. Ising Model
Ising model is important to model in statistical mechanics, which we can use in many fields [15,16,17,18]. usually used to explain the magnetization, liquid/gas cohabitation, and analysis as many papers[18].
Mello and others [19,20,21,22], work on the modification of the Ising-model to the Covid-19 spread, to describe the number of infections and fatality.
o explain the distinction between two persons: A with infected covid-19 and B non-infected covid-19, without external reasons, we know the Schelling model[23], on the Ising model with a square-lattice at zero temperature, thus this version of this model goes to small Nodes[24-33].
If there is physical distancing between person A who is infected and person B not infected then person B will not be infected unless there is no physical distancing between both of them then person be can easily get the infection from A.
n this way, we can describe the diffusive epidemic process in small groups and large groups, thus we consider the diffusive epidemic process coupled to the Ising model.
In our research, we look for all people which stand face to face as a network, and the persons with COVID-19 or not. here, imagine the first infected person [patient zero] is in contact with other people and fails to take proper precautions [social distancing, face covering, hand hygiene, etc. The members of this group who are infected by the virus may transmit it to relatives, friends, and other contacts, and these, in turn, may spread it to others, forming a ‘contact network’ that corresponds to a Bethe lattice in condensed matter physics.
Here, the celebrated Ising model will be presented in some detail we remember Ising model, which contacts on nearest neighbors, the Hamiltonian of a linear chain of N spins[19] given by:
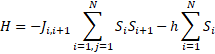
where Ji,i+1 is the coupling constant between neighboring magnetic moments on sites i and i+1, Si (Si+1) represents the spin on a site i (i + 1), and h represnted to the longitudinal applied magnetic field.
Square lattice, where the set of directions for n = 2 (i.e., the 2-dimensional Cartesian space), the set of direction vectors is: {(1,0), (-1,0), (0,1), (0,-1)}. Thus the neighbors of the node (1,1) are {(2,1), (0,1), (1,2), (1,0)} and the neighbors of the another node (2,1) are {(3,1),(1,1),(2,2),(2,0)}, as shown by the diagram:
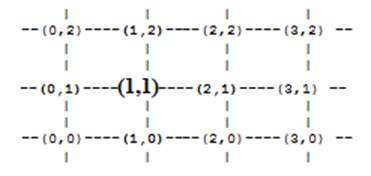
Figure (1): Distribution of neighbors in a square lattice for site (1,1).
2.2. Model and Simulation
In our study, the time unit in our simulation is in minutes, because exposure to cases just by standing near infected people (person with person as a neighbor), and we take (1 hour equal to 60min., 12 hours as = 720min., 24hour = 1440, and one week = 10080), and the carrier medium (external magnetic field: ±h) by two values which are randomly low (0.10) or high (0.90).
Here, the room temperature (temperature T) has two values, low temperature 2.0K, which means the air temperature is low, and the higher temperature means the air temperature is high.
And low temperatures prefer to live with their families and not mix with other people.
In our study, must be confirmed that the coupling constant Ji,i+1 which is also called the exchange coupling constant, will be used to simulate the connection between the persons who have COVID-19 and are healthy.
By using the random- field Ising model to distinguish between a patient with Covid -19 and a healthy person at one T, which indicates to the carrier medium where for a small external magnetic field (h=0.1, the carrier medium) the medium should be fresh and well ventilated, and for high external magnetic field (h=0.9, the carrier medium) should be polluted and without ventilation. At lower and higher temperatures we present simulation with a patient and healthy person for different finite times.
A square lattice taken with size 100x100 which is indicated to study samples because all mixed groups can't be larger than this number, also we can use a large number if we need as 500x500.
3. Results and Discussion
We tested here growth of domains of groups in a small random field of 0.10, and a low temperature of 2.0K at different times (1-hour, 12 hour, 24 hour, and 7 days).
Our result of the simulation are shown in Figs. 1(a –d), indicate that increasing in the number of infected persons with COVID-19 leads to the coverage of many areas when time increases i.e. the number of infected people is directly proportional when the time is increasing.
Zabarsky [35] detect the percentage for healthcare staff which infection SARS-CoV-2 and had higher-risk at work environment by 25% positive result with exposure time more than 15 minutes and distance 6 feet distributed 18 cases exposure to COVID-19 patients and 6 to infected personnel
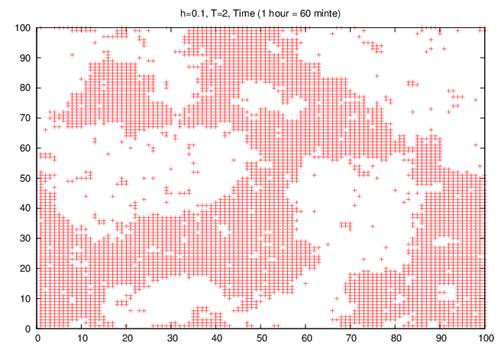
(1-a)
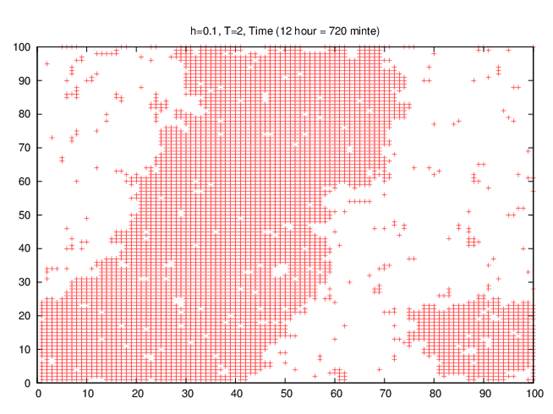
(1-b)
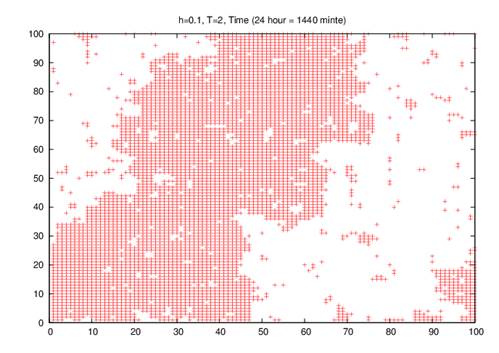
(1-c)
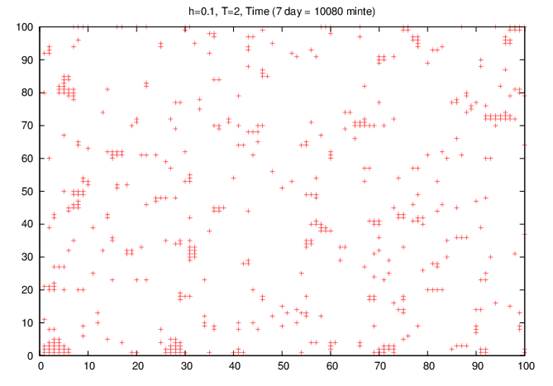
(1-d)
Fig. 1. Simulation of the Ising model simulation atr different times (a) 60 minutes, (b) 720 minutes, (c) 1440 minutes, and (d) 10080 minutes per site on 100 X 100 square lattice at kBT/J = 2 in a small random field of 0.10.
Figure 1-d shows that after a long time the infected groups begin to fade and appear as small infected numbers, which shows the formation of autoimmune against the disease (COVID-19).
Now, the growth of domains of groups in a large random field of h= 0.90, and low room temperature of 2.0K at different times (1 hour, 12 hours, 24 hours, and 7 days) and our results as shown in Figs. 2 (a –d), but the decrease in the number of cases when the time increasing, and the number of people with Covid-19id decreasing has clearly been observed.
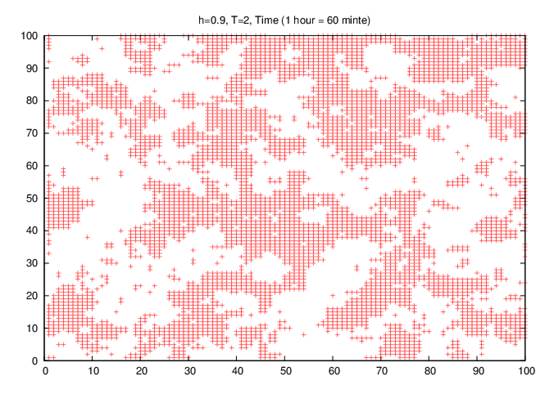
2-a 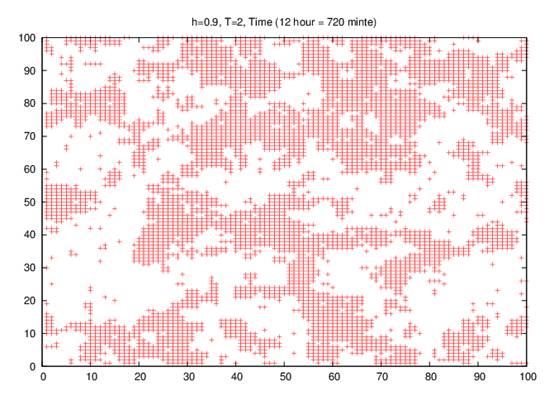
2-b
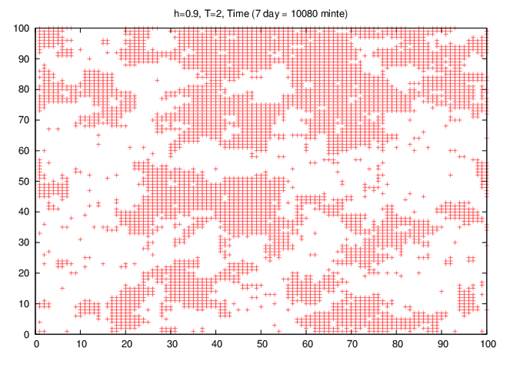
(2-c)
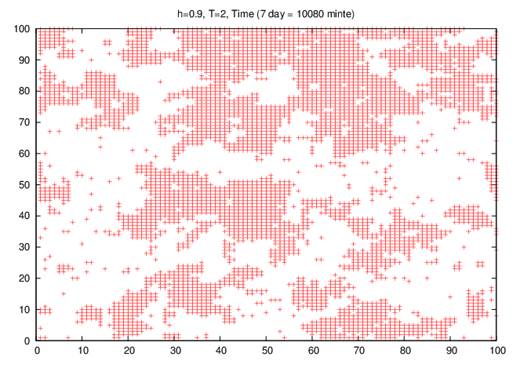
2-d))
Fig. 2. Simulation of Ising model at different times (a) 60 minutes, (b) 720 minutes, (c) 1440 minutes and (d) 10080 minutes on the site on 100 X 100 square lattice at kBT/J = 2 in a large random field of 0.90.
Now, we used high room temperature (99K) with the small external magnetic field (h = 0.10), no segregation has been observed between the nodes as shown in figure 3. It has also occurred at the high room temperature (99K), and with a high external magnetic field (h = 0.90) where there is no segregation between the nodes as we cannot differentiate between large infected groups and large uninfected groups as displayed in figure 4.
In this article, we used lower room temperature (2.0) with carrier medium (h=0.1, the medium should be fresh and well ventilated), thus we have non-growing domains in Infected cases, but for a lower room temperature (2.0) with carrier medium (h=0.9, should be polluted and without ventilation), there is growing domains which mean that collected for infected cases.
In another study, Sera et al[37] inform that the COVID-19 increased incrementally under lockdown between 2.5 and 10 °C. After that, there are balance between the number of COVID-19 patients and non-patients with slight changes between 10 and 25 °C. Above 26 °C to 37 °C, there are incrementally decrease in COVID-19 cases. after 37 °C, the positive cases will be zero
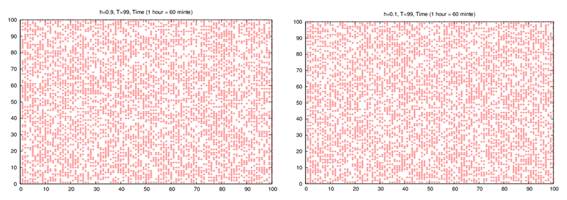
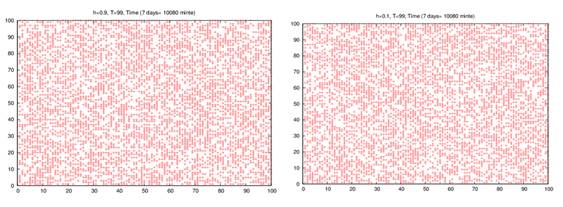
Fig. 3. Ising model simulation configurations after different times (60 minutes, 10080 minutes) per site on 100 X 100 square lattice at kBT/J = 99 in a small random and larger field equal (0.10 & 0.90).
lately, the COVID-019 has in all world. Gaza Strip is located on the south-eastern side of the Mediterranean Sea and housing more than 2 million Palestinians in only 365 km2 of land. Gaza Strip is considered to be one of the most densely populated urban areas all over the world, with nearly 5,479 persons per square meter [38]. The population density makes it more at risk for COVID-19.
While the first local confirmed case was recorded on the 24th August 2020, since that time, the number of confirmed cases increased sharply to 342, 362 coronavirus cases and more than 3824 deaths by the 25th of June, [36].
Now, we take the real infected of COVID-19 on Palestine ( West Bank and Gaza Strip) as posted on the website of the Ministry of Health [24] on the months 1-2-3-4/2021, as posted in figure(4-a-b-c-d), we see that when the government on the Gaza Strip and the West Bank does not take measures to limit the spread of the disease, such as closing, preventing movement and preventing mixing, we see an increase in the rate of infected people, but when the government takes measures and prevents people from mixing, the infections decrease significantly.
For more details, in 1-2021, there was a decrease in the number of infected cases, as is evident in figure (4-a), because of the tightening of preventive measures taken by the government, but with the laxity of these procedures and the entry of the third wave of COVID-19, the number of infected cases began to increase, as shown in figure ( 4-b), in 3-2021, the rate of infection continued to increase and maintained a high rate, as shown in figure(4-c), thus government implements strict measures such as (preventing the movement of cars at night, a comprehensive closure of shops and institutions on Fridays and Saturdays, disrupting schools, universities, and kindergartens, closing popular markets, ensuring non-mixing and wearing the muzzle only in closed and crowded places), which leads to a decline in the number of infected people per day as shown in figure4-d.
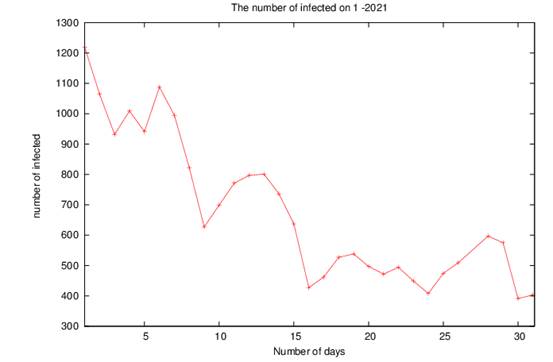
4-a
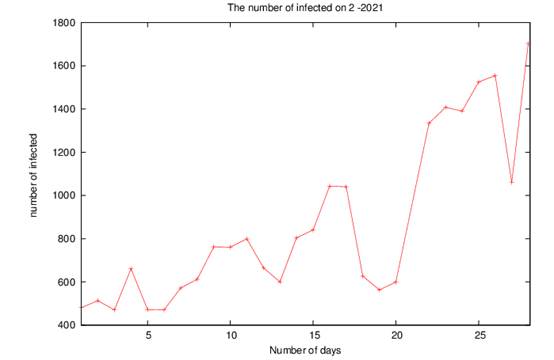
4-b
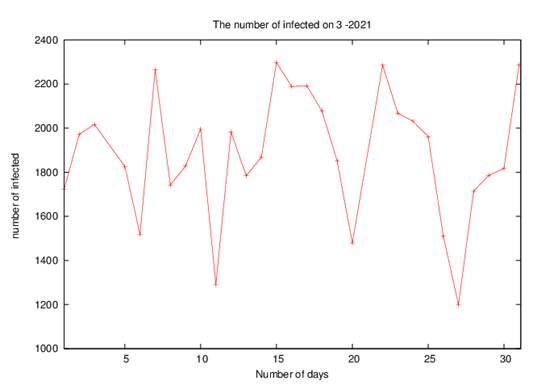
4-c
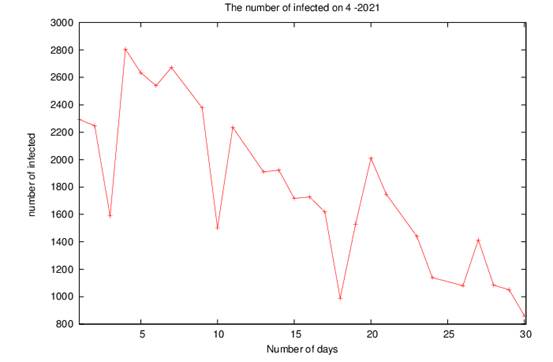
4-d
Fig. 4. Number of infected versus number of days on the moths a) 1-2021 b) 2-2021 c0 3-2021 d) 4-2021 on Gaza Strip and West Bank.
Now, we will draw a brief picture of the total number of infected cases from the start of the Coronavirus pandemic 3/2020 until the end of the month 10/2021 to see how the rate of infected cases increases when mixing and not adhering to safety standards and how they are reduced upon adherence to preventive measures as shown in fig.(5).
The total number who received anti-Coronavirus vaccines in the West Bank and Gaza Strip reached 481,392 of whom 339,082 received both doses of the vaccine. The total number of vaccinated citizens in the West Bank: 416,198 and in the Gaza Strip: 65,194[36].
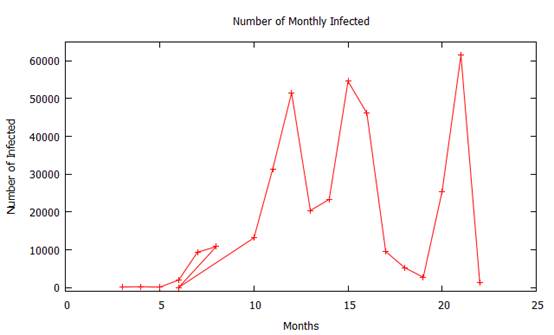
Fig. 5. Number of infected versus number of moths ( 3/2020-10/2021) on Gaza Strip and West Bank.
4. Conclusion
In conclusion, the main result in this study which had obtained related to the lockdown countries policies at national strategies under emergency status for COVID-19 virus and the optimum time to activate the lockdown
Thus, we must keep the air clean and fresh, and there must be a distance between the infected and the carriers, and if the people, with COVID-19 or not, are by the applicative and respect the social distance, the spread of the disease is controlled.
It is possible to coexist with COVID19, but we have to take the necessary precautions, and reventive measures such as spacing, wearing masks, and staying in a clean, pure, and changing atmosphere.
5. Acknowledgement
The authors thank Prof. Mariano de Souza for his valuable contribution and for providing many serious suggestions and discussions
References
[1] S. E. Park, “Epidemiology, virology, and clinical features of severe acute respiratory syndrome -coronavirus-2 (SARS-CoV-2; coronavirus disease-19),” Clin. Exp. Pediatr. 63, 119 (2020).
[2] C. Wang, Z. Liu, Z. Chen, X. Huang, M. Xu, T. He, and Z. Zhang, “The establishment of reference sequence for SARS-CoV-2 and variation analysis,” J. Med. Virol. 92, 667 (2020).
[3] X. Jiang, S. Rayner, and M. H. Luo, “Does SARS-CoV-2 has a longer incubation period than SARS and MERS?,” J. Med. Virol. 92, 476–478 (2020).
[4] WHO (World health Organization) (2021) Retrieved on 25june 2021 from https://www.who.int/emergencies/diseases/novel-coronavirus-2019
[5] S. Sanche, Y. T. Lin, C. Xu, E. Romero-Severson, N. Hengartner, and R. Ke,“High contagiousness and rapid spread of severe acute respiratory syndrome coronavirus 2,” Emerg. Infect. Dis. 26(7), 1470–1477 (2020).
[6] X. M. Rong, L. Yang, H. D. Chu, and M. Fan, “Effect of delay in diagnosis on transmission of COVID-19,” Math. Biosci. Eng. 17, 2725–2740 (2020).
[7] F. Rahimi and A. TalebiBezmin Abadi, “Practical strategies against the novel coronavirus and COVID-19-the imminent global threat,” Arch. Med. Res. 51(3), 280–281 (2020).
[8] M. A. SUMOUR, A. H. El-ASTAL, M. A. RADWAN, and M. M. SHABAT, International Journal of Modern Physics C Vol. 19, No. 4 (2008) 637-645.
[9] M. A. SUMOUR and M. A. RADWAN, International Journal of Modern Physics C, Vol. 23, No. 9 (2012) 1250062 (6 pages).
[10] Muneer A. Sumour, and M. M. Shabat, Islamic University Journal, IUG Journal of Natural and Engineering Studies, Vol 28, No 1,(2020), pp 46-51.
[11] M. A. Radwan, M. A. Sumour, A. H. El-Astal and M. M. Shabat, International Journal of Recent advances in Physics( IJRAP) Vol.2, No.1(2013).
[12] M.A. Sumour, M.A. Radwan, M.M. Shabat, IUG Journal of Natural and Engineering Studies, Vol.20, No.2, Pages( 15-28),(2012)
[13] M. A. SUMOUR, M. A. RADWAN, M. M. SHABAT, International Journal of Modern Physics C, Vol. 22, No. 12(1357-1360) Pages (2011) .
[14] M. A. SUMOUR, A. H. El-ASTAL, M. M. SHABAT and M. A. RADWAN International Journal of Modern Physics C, Vol. 18, No. 11 (2007) 1717-1723.
[15] T. Ezaki, T. Watanabe, M. Ohzeki, and N. Masuda, “Energy landscape analysis
of neuroimaging data,” Philos. Trans. A: Math. Phys. Eng. Sci. 375, 20160287 (2017).
[16] C. Ma, H. H. Zhang, and X. Wang, “Machine learning for big data analytics in plants,” Trends Plant Sci. 19, 798–808 (2014).
[17] M. Hogyoku, “Criticality found in a model for orientational ordering of protein arrays,” Adv. Biophys. 34, 55–68 (1997).
[18] M. Kawamura, K. Hayashi, T. Uezu, and M. Okada, “Statistical mechanical evaluation of a spread-spectrum watermarking model with image restoration,” Phys. Rev. 99, 062132 (2019)
[19] Isys F. Mello, Lucas Squillante , Gabriel O. Gomes , Antonio C. Seridonio , Mariano de Souza, Physica A 573 (2021) 125963.
[20] Grassly, N., Fraser, C. Mathematical models of infectious disease transmission. Nat Rev Microbiol 6, 477–487 (2008). https://doi.org/10.1038/nrmicro1845
[21] Mohamadou, Y., Halidou, A. &Kapen, P.T. A review of mathematical modeling, artificial intelligence and datasets used in the study, prediction and management of COVID-19. Appl Intell 50, 3913–3925 (2020). https://doi.org/10.1007/s10489-020-01770-9.
[22] Liu, M., Huo, P., Zhu, W. et al. Broadband
generation of perfect Poincaré beams via dielectric spin-multiplexed
metasurface. Nat Commun 12, 2230 (2021).
https://doi.org/10.1038/s41467-021-22462-z
[23] T. C. Schelling, J. Math. Sociol. 1, 143 (1971); M. Fossett, ibid. 30, 185
(2006).
[24] D. Vinkovic and A. Kirman, Proc. Natl. Acad. Sci. USA 103, 19261 (2006).
[25] D. Stau_er and S. Solomon, Eur. Phys. J. B 57, 473 (2007).
[26] R. Albert and A. L. Barabasi, Rev. Mod. Phys. 74, 47 (2002).
[27] David P. Landau and Kurt Binder, A Guide to Monte Carlo Simulation in Statistical Physics (Cambridge University Press, 2002).
[28] A. L. Barabasi, Linked, Perseus (Cambridge, 2002).
[29] A. L. Barabasi, Science 325, 412 (2009).
[30] R. Albert and A. L. Barabasi, Rev. Mod. Phys. 74, 47 (2002).
[31] A. L. Barabasi, Linked, Perseus (Cambridge, 2002).
[32] A. L. Barabasi, Science 325, 412 (2009).
[33] David P. Landau and Kurt Binder, A Guide to Monte Carlo Simulation in Statistical Physics (Cambridge University Press, 2002).
[34] Muneer A. Sumour, F.W.S. Lima, M.M. Shabat, D. Stauffer,Physica A, Volume 505, 1 September 2018, Pages 1163-1169
[35] Zabarsky TF, Bhullar D, Silva SY, Mana TSC, Ertle MT, Navas ME, Donskey CJ 2020. What are the sources of exposure in healthcare personnel with coronavirus disease 2019 infection?. .Am J Infect Control. 2021 Mar;49(3):392-395.
[36] MOH (Ministry of Health) (2021) Retrieved on 25june 2021 from http://site.moh.ps/index/covid19/.
[37] Vicedo-Cabrera, A.M., Scovronick, N., Sera, F. et al. The burden of heat-related mortality attributable to recent human-induced climate change. Nat. Clim. Chang. 11, 492–500 (2021). https://doi.org/10.1038/s41558-021-01058-x
[38] Anon. United Nations Country Teamin the Occupied Palestinian Territories, Gaza 10 years later. July. Available from:. 2017. https://unsco.unmissions.org/sites default/files/gaza_10_years_later_-_11_july_2017.pdf.
Authors
 Dr. Muneer A.
Sumour
was born in 1967, Palestinian Territories. In 1996 he has got his B.Sc in
Physics from Islamic University in Palestine. In 2005 he obtained the M.Sc. in
Computational statistical Physics from Islamic University in Palestine. In 2008
he was awarded the Ph.D. Computational statistical Physics from the Ein shams
University of Egypt. In 1998 he was appointed as an lecture in physics at department
of physics, Al-Aqsa University, Palestine. He published various refereed papers
on Computational statistical Physics and other related topics and participated
in many conferences.
Dr. Muneer A.
Sumour
was born in 1967, Palestinian Territories. In 1996 he has got his B.Sc in
Physics from Islamic University in Palestine. In 2005 he obtained the M.Sc. in
Computational statistical Physics from Islamic University in Palestine. In 2008
he was awarded the Ph.D. Computational statistical Physics from the Ein shams
University of Egypt. In 1998 he was appointed as an lecture in physics at department
of physics, Al-Aqsa University, Palestine. He published various refereed papers
on Computational statistical Physics and other related topics and participated
in many conferences.
In 2011 he start to work in deanship of quality assurance as head of department of accreditation and academic quality until 2017,in 2018 he worked as a director of Planning & development dean in Deanship of Planning, Development and Quality Assurance until now.
He Participated in the publication of a special paper applying the comprehensive quality standards at Al-Aqsa University.
Email: ma.sumoor@alaqsa.edu.ps
Mobil: 00972599470729
 Professor Dr. Mohammad M. Shabat was born in Beit
Hanoun, Gaza Strip, Palestine in 1960. He received his B.Sc. in Physics from
Al-Aazhar University, Cairo, Egypt in 1984 and the Ph.D. degree from the
University of Salford, the U.K. in 1990. He was a Research Fellow at the
University of Manchester Institute of Science and Technology, UK, from 1989 to
1992. In April 1992, he joined the Physics Department at the Islamic University
of Gaza (IUG) as an Assistant Professor of physics. He became an Associate
Professor in 1996 and a Professor of Physics in 2000. In the period 2001-2005,
he was the Vice President for Administrative Affairs at IUG and the Vice
President for the Academic Affairs at the IUG between 2009-2013. He was awarded
the Shoman Prize for a Young Arab Scientist (Jordan) in 1995, and the Humboldt
Research Fellowships in 1998-99 at the Center of Semiconductor Technology and
Opto-electronics, Duisburg-Essen University, Germany. He was a visiting
scientist at Bochum University, Germany, in 1994; at the Institute National
Polytechnic de Grenoble, (INPG), France, in 1995; at Salford University, U.K,
in 1997; ICTP, Trieste, Italy, in 1996,1997 and 1998, 2000, 2001, 2003, 2004;
Duisburg-Essen University, Germany, in1998, 1999 and 2002, 2003, 2004 and 2006,
and 2007; the Technical University of Warsaw in 2012; Frankfort University in
2012 and the Institute of Energy Research and Physical Technologies (IEPT) at
the Clausthal Technical University (TUC) in 2015, 2018, 2019. From 2006-2008,
Prof. Shabat was a visiting Professor at Max Planck Institute for the Physics
of Complex Systems, Dresden, Germany. Professor Shabat had received
"Galileo Galilei" Award of the International Commission of Optics
(affiliated to ICSU and IUPAP) in 2006. He was the Vice President for the
Research and Graduate Studies at the IUG between 2013-2015. Professor Shabat
became the first Distinguished Professor in the IUG in 2011. He was awarded the
Distinguished Scholar Award, the Arab Fund Fellowship Program, Kuwait, 2007. He
had been awarded the ISESCO Science Prize, 2010. He published more than 400
papers in international journals in socio-physics, optical science, physics,
mathematics and education and presented many papers at local and international
conferences. His research interests include solar cells, nonlinear optical
sensor, Renewable Energy, opto-electronics, magneto static surface waves,
numerical techniques, mesoscopic systems, energy, applied mathematics,
Nanotechnology and physics education. He supervised more than 40 postgraduate
students (M.Sc. and Ph.D.) in mathematics and physics at Palestinian, Sudanese,
Algerian and Egyptian universities. Recently he has established a Palestinian
Optical Society (POS). He is an external examiner for BSc examinations, M.Sc.
dissertation and Ph.D. theses in physics and mathematics at Palestinian and
Egyptian universities. He is a senior member of IEEE, a member of the Optical
Society of America, a fellow of the World Academy of Sciences for the
advancement of science in developing countries (TWAS) and a fellow of the Islamic
World Academy of Sciences (IAS).He was a Commissioner of the Accreditation
and Quality Commission, Ministry of Higher Education, Palestine, 2011- 2017, a
Member, Management
Board, the Euro-Mediterranean University (EMUNI University), Slovenia, Elected
2013, and a Member, the Senate, The Euro-Mediterranean University (EMUNI
University), Slovenia, 2013-2019, Vice Chairman, the Senate, the Board of
Trustee, University of Palestine, Gaza, Gaza Strip, Palestine, 2014-2018, Member of the
Mediterranean Institute of Fundamental Physics, Rome, Italy, 2013, Member of the
Search Commission for the Post of President, the Euro-Mediterranean University
(EMUNI University), Slovenia, 2013, Member, and a member, Habilitation Commission, the
Euro-Mediterranean University (EMUNI University), Slovenia, 2013-2-19.
Professor Dr. Mohammad M. Shabat was born in Beit
Hanoun, Gaza Strip, Palestine in 1960. He received his B.Sc. in Physics from
Al-Aazhar University, Cairo, Egypt in 1984 and the Ph.D. degree from the
University of Salford, the U.K. in 1990. He was a Research Fellow at the
University of Manchester Institute of Science and Technology, UK, from 1989 to
1992. In April 1992, he joined the Physics Department at the Islamic University
of Gaza (IUG) as an Assistant Professor of physics. He became an Associate
Professor in 1996 and a Professor of Physics in 2000. In the period 2001-2005,
he was the Vice President for Administrative Affairs at IUG and the Vice
President for the Academic Affairs at the IUG between 2009-2013. He was awarded
the Shoman Prize for a Young Arab Scientist (Jordan) in 1995, and the Humboldt
Research Fellowships in 1998-99 at the Center of Semiconductor Technology and
Opto-electronics, Duisburg-Essen University, Germany. He was a visiting
scientist at Bochum University, Germany, in 1994; at the Institute National
Polytechnic de Grenoble, (INPG), France, in 1995; at Salford University, U.K,
in 1997; ICTP, Trieste, Italy, in 1996,1997 and 1998, 2000, 2001, 2003, 2004;
Duisburg-Essen University, Germany, in1998, 1999 and 2002, 2003, 2004 and 2006,
and 2007; the Technical University of Warsaw in 2012; Frankfort University in
2012 and the Institute of Energy Research and Physical Technologies (IEPT) at
the Clausthal Technical University (TUC) in 2015, 2018, 2019. From 2006-2008,
Prof. Shabat was a visiting Professor at Max Planck Institute for the Physics
of Complex Systems, Dresden, Germany. Professor Shabat had received
"Galileo Galilei" Award of the International Commission of Optics
(affiliated to ICSU and IUPAP) in 2006. He was the Vice President for the
Research and Graduate Studies at the IUG between 2013-2015. Professor Shabat
became the first Distinguished Professor in the IUG in 2011. He was awarded the
Distinguished Scholar Award, the Arab Fund Fellowship Program, Kuwait, 2007. He
had been awarded the ISESCO Science Prize, 2010. He published more than 400
papers in international journals in socio-physics, optical science, physics,
mathematics and education and presented many papers at local and international
conferences. His research interests include solar cells, nonlinear optical
sensor, Renewable Energy, opto-electronics, magneto static surface waves,
numerical techniques, mesoscopic systems, energy, applied mathematics,
Nanotechnology and physics education. He supervised more than 40 postgraduate
students (M.Sc. and Ph.D.) in mathematics and physics at Palestinian, Sudanese,
Algerian and Egyptian universities. Recently he has established a Palestinian
Optical Society (POS). He is an external examiner for BSc examinations, M.Sc.
dissertation and Ph.D. theses in physics and mathematics at Palestinian and
Egyptian universities. He is a senior member of IEEE, a member of the Optical
Society of America, a fellow of the World Academy of Sciences for the
advancement of science in developing countries (TWAS) and a fellow of the Islamic
World Academy of Sciences (IAS).He was a Commissioner of the Accreditation
and Quality Commission, Ministry of Higher Education, Palestine, 2011- 2017, a
Member, Management
Board, the Euro-Mediterranean University (EMUNI University), Slovenia, Elected
2013, and a Member, the Senate, The Euro-Mediterranean University (EMUNI
University), Slovenia, 2013-2019, Vice Chairman, the Senate, the Board of
Trustee, University of Palestine, Gaza, Gaza Strip, Palestine, 2014-2018, Member of the
Mediterranean Institute of Fundamental Physics, Rome, Italy, 2013, Member of the
Search Commission for the Post of President, the Euro-Mediterranean University
(EMUNI University), Slovenia, 2013, Member, and a member, Habilitation Commission, the
Euro-Mediterranean University (EMUNI University), Slovenia, 2013-2-19.
Telefax: +972 8 2863552 Email: shabat@mail.iugaza.edu.ps.
 Last Name: El Aila
Last Name: El Aila
First Name: Nabil
Date of birth: November 7, 1967
Place of birth: Gaza, Palestine
Nationality: Palestinian
Education
1990-1994: Bachelor in Medical Technology, Islamic University, Gaza, Palestine
General grade: Very Good
2000-2002: Master in Molecular Biology, Vrije University Brussel , Belgium
General grade: Great Distinction
2006-2011: Doctoral of Biomedical Sciences (Molecular Microbiology)
Faculty of Medicine – Ghent University – Belgium.
E-mail: na.elaila@alaqsa.edu.ps
